feremet.blogg.se - Travelling salesman problem using dynamic programming in c

That helps to move vigorously in early steps, and cautiously in later steps. The search step must be reduced in size while the search process is moving forward and getting close to the final result.

The moving direction must be probabilistically determined in each step with the hope of not getting trapped in a local optimum and moving toward the global optimum.

The SA method has two major rules explained below. The lesson that optimization experts learned from the annealing mechanism is to enforce more control over the search process contrary to the gradient descent algorithm with fixed rules. But, how does this map to an optimization problem? Annealing refers to a controlled cooling mechanism that leads to the desired state of the material. Simulated Annealing or SA is a heuristic search algorithm that is inspired by the annealing mechanism in the metallurgy industry. The DP method can guarantee the global optimum but it just needs much time and computational power that we mostly can not afford in real-world problems. Suggestion- If you want to solve traveling salesman problem with a large number of cities the dynamic programming method is not the best choice.

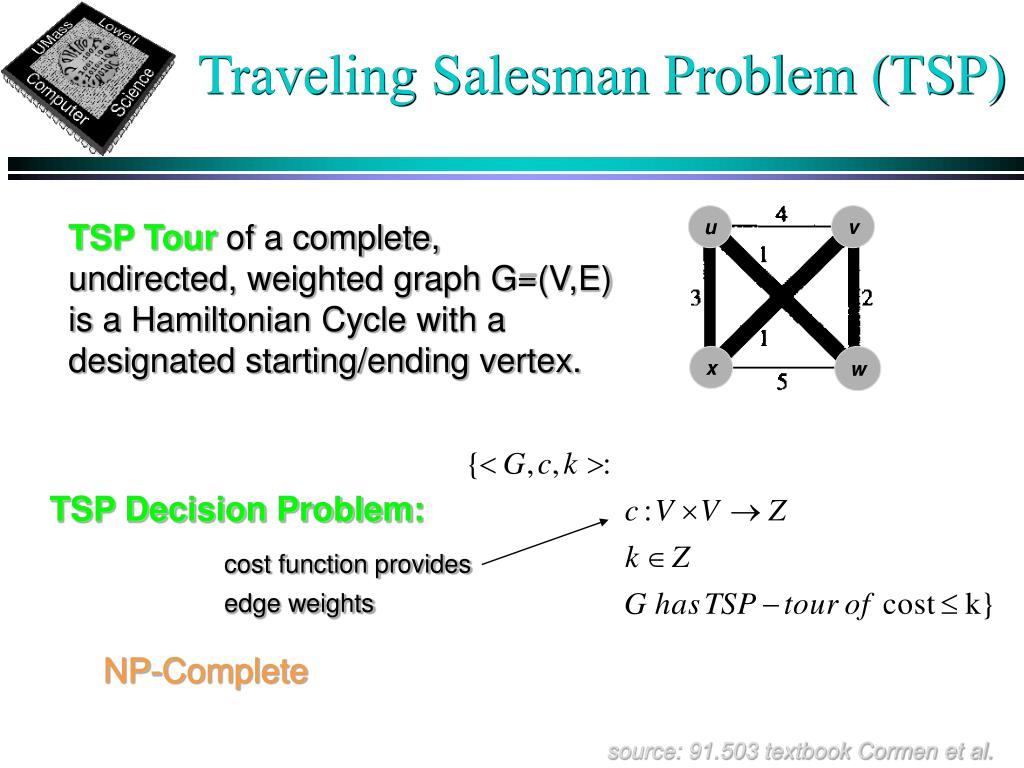
However, the memoization technique with a large number of cities needs a 2^N × 2^N matrix that can not be easily handled in memory. To optimize the DP method, I could have used the memoization technique. That is, the time complexity significantly increases even with a small increment in the number of cities. This number increases to almost 13 seconds (~60 times greater) with 15 cities. TSP with 10 cities can be solved by a DP method in almost 0.2 seconds using intel core i7. To give you a hint of how this time complexity increases, let me share my experiments. The time complexity with the DP method asymptotically equals N² × 2^N where N is the number of cities. However, its time complexity would exponentially increase with the number of cities. The dynamic programming or DP method guarantees finding the best answer to TSP.